3. Trigonometry

d. Trig Identities

There are three trig identities whose proofs involve a little more geometry than the previous ones. They are the Law of Sines and the Law of Cosines (discussed here) and the Sum of Angles Formulas (discussed on the next page).

3. Law of Sines and Law of Cosines

Given a triangle \(\triangle ABC\), as long as there is no confusion, we will denote the angle at each vertex by the same letter as the vertex. For example, the angle at the vertex \(B\) has measure \(B\).

Law of Sines

If a triangle \(\triangle ABC\) has opposite sides with lengths \(a\), \(b\) and \(c\) resp., then \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] Proof \(\Leftarrow\Leftarrow\) Read it! It's straightforward.

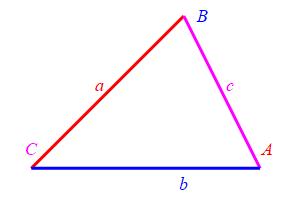
Drop a perpendicular from \(B\) to the opposite side \(CA\). Let \(P\) be the point of intersection which is called the foot of the perpendicular and let \(h\) be the length of this perpendicular. Looking at the right triangle \(\triangle APB\), we observe \(\sin A=\dfrac{h}{c}\). Similarly, looking at the right triangle \(\triangle CPB\), we observe \(\sin C=\dfrac{h}{a}\). Solving each equation for \(h\) and equating, we get: \[ h=c\sin A=a\sin C \] Dividing by \(ac\) gives the result: \[ \dfrac{\sin A}{a}=\dfrac{\sin C}{c} \]

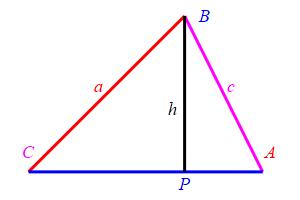
If we drop the perpendicular from \(A\) instead of \(B\), we would conclude: \[ \dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] Together, these give the theorem.

Actually, to have a full proof, we still need to check the case where the foot of the perpendicular is not between \(C\) and \(A\). Extra Case

Extra Case where \(P\) is not between \(C\) and \(A\)

For the triangle \(\triangle APB\), we still have \(\sin A=\dfrac{h}{c}\). For the triangle \(\triangle CPB\), we also need to use a Supplementarity Identity: \[ \sin C=\sin(\pi-C)=\dfrac{h}{a} \] We still conclude: \[ h=c\sin A=a\sin C \] and \[ \dfrac{\sin A}{a}=\dfrac{\sin C}{c} \]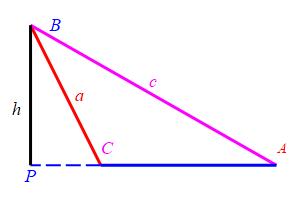

Law of Cosines

If a triangle \(\triangle ABC\) has opposite sides with lengths \(a\), \(b\) and \(c\) resp., then \[ c^2=a^2+b^2-2ab\cos C \] and similarly for the other two sides: \[ a^2=b^2+c^2-2bc\cos A \] \[ b^2=a^2+c^2-2ac\cos B \] Proof \(\Leftarrow\Leftarrow\) Read it! It's straightforward.

Drop a perpendicular from \(B\) to the opposite side \(CA\). Let \(P\) be the foot of the perpendicular and let \(h\) be the length of this perpendicular. Let \(r\) be the length of the segment \(CP\). Then the length of the segment \(PA\) is \(b-r\). Applying the Pythagorean Theorem to the triangle \(\triangle CPB\), we observe \[ h^2=a^2-r^2 \] Similarly, for the triangle \(\triangle APB\), we have \[ h^2=c^2-(b-r)^2=c^2-b^2+2br-r^2 \]

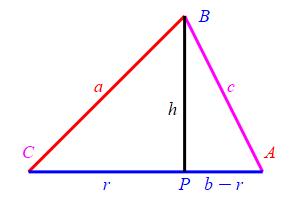
Equating these two formulas for \(h^2\), we get: \[ c^2-b^2+2br-r^2=a^2-r^2 \] or \[ c^2=a^2+b^2-2br \] Finally, we look at the triangle \(\triangle CPB\) again. We see \(\cos C=\dfrac{r}{a}\). So \(r=a\cos C\) and \[ c^2=a^2+b^2-2ab\cos C \]

Actually, to have a full proof, we still need to check the case where the foot of the perpendicular is not between \(C\) and \(A\). Extra Case

Extra Case where \(P\) is not between \(C\) and \(A\)

For the triangle \(\triangle CPB\), we still have \(h^2=a^2-r^2\). For the triangle \(\triangle APB\), we now have: \[ h^2=c^2-(b+r)^2=c^2-b^2-2br-r^2 \] Equating these two formulas for \(h^2\), we get: \[ c^2-b^2-2br-r^2=a^2-r^2 \] or \[ c^2=a^2+b^2+2br \]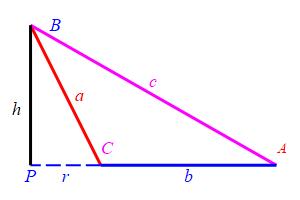

Finally, we look at the triangle \(\triangle CPB\) again. We again need to use a Supplementarity Identity: \[ \cos C=-\cos(\pi-C)=-\,\dfrac{r}{a} \] So \(r=-a\cos C\) and \[ c^2=a^2+b^2-2ab\cos C \]

First, an example which just uses the Law of Sines.

Two angles of a triangle are \(A=45^\circ\) and \(B=30^\circ\) and the side between them has length \(c=10\,\text{cm}\). Find the third angle and the lengths of the other two sides.
You may use a calculator. Give answers to \(3\) decimal places.

The sum of the angles must be \(180^\circ\). So the third angle is: \[ C=180^\circ-A-B=180^\circ-45^\circ-30^\circ=105^\circ \] The other two sides may be found by using the Law if Sines: \[ \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} \] Since \(C=105^\circ\) and \(c=10\), we have: \[ \dfrac{c}{\sin C}=\dfrac{10}{\sin 105^\circ}=10.353 \] and so: \[\begin{aligned} a&=\dfrac{c}{\sin C}\sin A=10.353\sin45^\circ=7.32\,\text{cm} \\[5pt] b&=\dfrac{c}{\sin C}\sin B=10.353\sin30^\circ=5.176\,\text{cm} \\ \end{aligned}\]

Now, an example which just uses the Law of Cosines.

Two sides of a triangle are \(a=3\,\text{in}\) and \(b=4\,\text{in}\) and the angle between is \(C=60^\circ\). Find the length of the third side.
You may use a calculator. Give answers to \(3\) decimal places.

Since \(\cos60^\circ=\dfrac{1}{2}\), the Law of Cosines tells us: \[\begin{aligned} c^2&=a^2+b^2-2ab\cos C \\ &=3^2+4^2-2\cdot3\cdot4\cos60^\circ=13 \\[5pt] c&=\sqrt{13}\,\text{in}\approx3.606\,\text{in}\\ \end{aligned}\]

Finally, an example which uses both the Law of Sines and the Law of Cosines. However, we first have a warning.

Caution: Recall that the Supplementarity Identity says \(\sin(\theta)=\sin(\pi-\theta)\). Further, the inverse function \(\arcsin z\), for positive \(z\), always produces an angle \(\theta\) in the interval \(0 \le \theta \le \dfrac{\pi}{2}\), i.e. an acute angle. (See the page on \(\arcsin\).) Consequently, when applying the Law of Sines, be aware that when solving the equation \[ \sin A=X \] (for some number \(X\)) there are two solutions: \[ A=\arcsin X \qquad \text{and} \qquad A=\pi-\arcsin X \] The first is acute and the second is obtuse. The correct one makes the angles add up to \(\pi\). Also note there can only be one obtuse angle in a triangle and it must be opposite the longest side. This will be demonstrated in the example:

Two sides of a triangle are \(5\,\text{cm}\) and \(8\,\text{cm}\) and the angle between them is \(45^\circ\). Find the length of the third side and the other two angles.
You may use a calculator. Give answers to \(3\) decimal places.

We let \(a=5\), \(b=8\) and \(C=45^\circ\). By the Law of Cosines, the length of the third side is: \[\begin{aligned} c&=\sqrt{a^2+b^2-2ab\cos C} \\ &=\sqrt{5^2+8^2-2(5)(8)\cos 45} \\ &=\sqrt{89-80\cos 45^\circ} \approx5.695 \end{aligned}\] By the Law of Sines, we know: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] Since \(C=45^\circ\) and \(c\approx5.695\), we have: \[ \dfrac{\sin C}{c}=\dfrac{\sin 45^\circ}{5.695}=0.124 \] and so: \[\begin{aligned} \sin A&=a\dfrac{\sin C}{c}=5(0.124)\approx 0.62 \\ \sin B&=b\dfrac{\sin C}{c}=8(0.124)\approx 0.992\\ \end{aligned}\] Since \(b=8\) is the longest side, the solutions are \[\begin{aligned} A&=\arcsin(0.62)=38.316^\circ \\ B&=\arcsin(0.992)=82.747^\circ\quad\text{or} \\ &=180^\circ-\arcsin(0.993)=97.253^\circ \end{aligned}\] The \(3\) angles must add up to \(180^\circ\). We try the acute \(B\): \[ A+B+C=38.316+82.747+45=166.06^\circ\ne180^\circ \] We try the obtuse \(B\): \[ A+B+C=38.316+97.253+45=180.57^\circ\approx180^\circ \] (There is a small amount of rounding error.) Therefore: \[ a=5\,\text{cm} \quad \text{and} \quad b=8\,\text{cm} \quad \text{and} \quad c=5.695\,\text{cm} \] \[ A=38.316^\circ \quad \text{and} \quad B=97.253^\circ \quad \text{and} \quad C=45^\circ \] (You might get slightly different answers due to rounding errors.)